12 Dec 2017. This article is now available on arXiv with more updates.
15 Nov 2017. General text improvements.
Approximate Computing (AC) is a wide spectrum of techniques that relax the accuracy of computation in order to improve performance, energy, and/or another metric of merit. AC exploits the fact that several important applications, like machine learning and multimedia processing, do not require precise results to be useful.
For instance, we can use a lower resolution image encoder in applications where high-quality images are not necessary. In a data center, this may lead to large savings in the amount of required processing, storage, and communication bandwidth.
Research interest in AC has been growing in recent years. I refer here to two recent surveys [1] [2] for a comprehensive treatment. In this article, I'll try to provide an introduction to this research field.
Basically, my discussion starts from the absolute beginning by motivating AC and discussing its research scope. Then, I discuss key concepts based on a proposed taxonomy. Finally, I further elaborate on nondeterministic AC, an AC category with unique opportunities as well as challenges.
Graduate students will, hopefully, find this introduction useful to catch up with recent developments.
Note that some of the ideas discussed here are based on a poster I presented at an AC workshop. The workshop was a satellite event to ESWEEK'16. Our extended abstract highlighted some AC challenges and opportunities in general. There, we argued that nondeterministic AC faces a fundamental control-flow wall which is bad news! The good news, however, is that there are still enough opportunities in deterministic AC to keep practitioners busy for the foreseeable future.
I shall elaborate on those issues and more in the following.
Motivation
So let's start by trying to answer the why and what questions for AC. Our concrete questions in this regard are:
- What motivates the recent academic interest in AC? In other words why do we need to care about AC more than before?
- What approximate computing really is? Note that AC is used in practice for decades already, so what makes recent academic proposals different?
In fact, research in AC can be motivated by two key concerns, namely, power and reliability.
Nowadays, the majority of our computations are being done either on mobile devices or in large data centers (think of cloud computing). Both platforms are sensitive to power consumption. That is, it would be nice if we can extend the operation time of smartphones and other battery powered devices before the next recharge.
Also, and perhaps more importantly, the energy costs incurred on data centers need to be reduced as much as possible. Note that power is one of (if not the) major operational cost of running a data center. To this end, algorithmic optimizations, dynamic run-time adaptation, and various types of hardware accelerators are used in practice.
Vector processors, FPGAs, GPUs, and even ASICs (like Google's recent TPU) are all being deployed in an orchestrated effort to optimize performance and reduce power consumption.
In this regard, the question that the AC community is trying to address is; can we exploit the inherit approximate results of some application to gain more power savings?
We move now to reliability concerns to further motivate AC. The semiconductor industry is aggressively improving it's production processes to keep pace with the venerable Moore's law (or maybe a bit slower version of it in recent years). Microchips produced with 10 nanometer processes are already shipping to production. Moving toward 7 nanometers and beyond is expected within the next 5 years according to the ITRS roadmap.
Such nanometer regimes are expected to cause a twofold problem. First, transistors can be more susceptible to faults (both temporary and permanent ones). For example, cosmic radiation can more easily cause a glitch in data stored in a Flip-Flop. Consequently, more investment might be necessary in hardware fault avoidance, detection, and recovery.
Second, feature variability between microchips or even across the same microchip can also increase. This means that design margins need to be more pessimistic to account for such large variability. That is, manufacturers have to allow for a wider margin for the supply voltage, frequency, and other operational parameters in order to keep the chip reliable while maintaining an economical yield.
In response to these reliability challenges, the AC community is investigating the potential of using narrower margins to operate microchips. However, hardware faults might occasionally propagate to software in this case. Therefore, the research goal is to ensure that such faults do not cause program outputs to diverge too much from the ideal outputs.
Such schemes can allow chip manufacturers to relax their investments in maintaining hardware reliability. More performance and power saving opportunities can be harnessed by moving to best-effort hardware instead [3].
Definition and scope
So far, we motivated the need for approximate computing. We move now to our second question; What is approximate computing in the first place?
Let's come back to our image encoding example. We know that applying any lossy compression algorithm (JPEG for example) to a raw image will result in an approximate image. Such compression often comes (by design) with little human perceptible loss in image quality. Also, image encoders usually have tunable algorithmic knobs, like compression level, to trade off image size with its quality.
Therefore, do not we already know how to do AC on images? Actually, instances of AC are by no means limited to image processing. AC is visible in many domains from wireless communication to control systems and beyond. In fact, one can argue that every computing system ever built did require balancing trade-offs between cost and quality of results. This is what engineering is about after all.
Indeed, approximate computing is already a stable tool in the engineering toolbox. However, it's usually applied manually leveraging domain knowledge and past experience. The main goal of recent AC research, I think, is to introduce automation to the approximation process. That is, the research goal is to (semi-) automatically derive/synthesize more efficient computing systems which produce approximate results that are good enough.
I shall elaborate on this point based on Figure (1). Consider for example that you have been given a computing system with a well-specified functionality. Such system can consist of software, hardware, or a combination of both. Now, your task is to optimize this system to improve its performance. How would you typically go about this task?
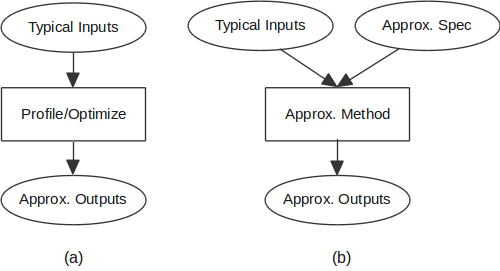
Figure (1): AC can be applied (a) manually in the usual profile/optimize cycle, or (b) automatically via an approximation method which may require providing an error quality specification.
Ideally, you start by collecting typical inputs which represent what you expect the system to handle in the real world. Then, based on those inputs, you attempt to profile the system to identify hot regions where the system spends most of the time. After that, the serious optimization work begins which might involve several system layers.
For example, in a software program, you will often need to modify the algorithms and data structures used. You might also go all the way down to the nitty-gritty details of improving cache alignment or 'stealing' unused bits in some data structures for other purposes.
This profile/optimize cycle continues until you either meet your performance target or you think that you have reached the point of diminishing returns. This optimization process is generally applicable to any computing system. However, with a system that can tolerate controllable deviations from its original outputs, you can go a bit further in your optimization.
Basically, AC is about this last mile in optimization. The research goal is to investigate automatic, principled, and ideally generic techniques to gain more efficiency by relaxing the exactness of outputs. The need for automation is obvious since manual approximation techniques can simply be regarded as 'business as usual' i.e., without clear improvement over the state of practice.
Furthermore, AC needs to guarantee, in a principled way, that the expected output errors will remain 'acceptable' in the field. That is, computing systems already struggle with implementation bugs. Therefore, it's difficult to adopt an AC technique that can introduce more bugs in the form of arbitrary outputs.
We come to the third criterion which is generality. I consider a technique to be generic if it is applicable to a wide spectrum of domains of interest to AC. For example, loop invariant code motion is a generic compiler optimization that applies to virtually any program from scientific simulations to high-level synthesis.
Generality, however, is more challenging to achieve in AC compared to the 'safe' optimizations used in compilers. A local AC optimization might introduce errors which are difficult to reason about when combined with other local optimizations. Note that the combined error observed on the global outputs might be composed of several local errors.
Actually, I'd argue that it's not feasible to target, to a satisfactory level, all three criteria. In other words, better automation and principled guarantees require compromising on generality. This can be achieved by embedding domain-specific knowledge in the AC technique. This seems to be a reasonable thing to do given the diversity of domains where AC is applicable.
A prime advantage of compromising on generality is that end users won't need to explicitly provide error quality specification, see Figure (1). Metrics of acceptable errors will be based on the specific domain. For instance, generalization error in machine learning and PSNR in image compression.
A taxonomy of approximate computing
The literature on approximate computing is large and growing. Also, it covers the entire system stack from high-level algorithms down to individual hardware circuits. It's difficult to make sense of all of these developments without introducing some sort of structure. In this section, I'll attempt such structuring based on the taxonomy depicted in Figure (2). Also, selected pointers to the relevant literature will be highlighted.
Basically, my hypothesis is that we can map any individual AC technique to a point in a three-dimensional space. The considered axes represent the approximation level, required run-time support, and behavior determinism respectively. Of course, there are papers on AC that combine several techniques in one proposal.
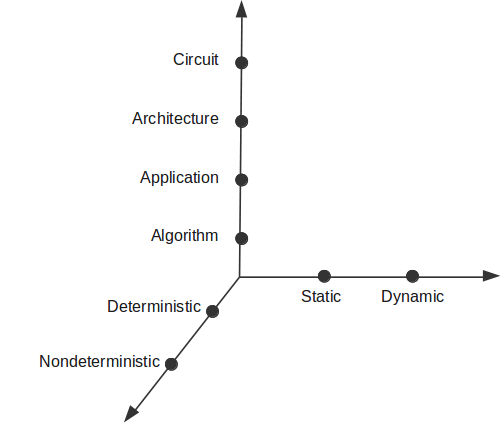
Figure (2): Proposed AC taxonomy. Expected cost of targeting a design point rises as we move away from the center.
The reader might be wondering why hardware circuits have been placed higher up while the algorithm level is at the bottom? The reason is simply the expected cost of targeting such a design point. In other words, I expect the implementation cost to increase as one explores design points further away from the center.
For instance, a system that involves dynamic run-time adaption, e.g., for error quality monitoring, is more complex, and thus more costly, to build and maintain compared to a static system. However, run-time adaptation might provide sufficient benefits to amortize the higher cost if designed with care.
Now, we move to the determinism axis. My classification is based on the usual determinism property. That is, an algorithm that returns the same output repeatedly given the same input is deterministic. Nondeterministic algorithms do not exhibit such output repeatability.
I further classify nondeterministic algorithms to partially and fully nondeterministic. These categories are based on the sources of nondeterminism in the algorithm and bug reproducibility. Nondeterministic AC will be discussed in more detail in the next section.
The axis of approximation level in Figure (2) has been (roughly) divided into 4 categories. At algorithm level, a given algorithm is kept intact. To implement approximation, one has to manipulate either the inputs or algorithm configurations (knobs or hyperparameters). An example of the former can be found in ApproxHadoop [4] where the authors utilized a statistical input sampling scheme in order to derive approximate results.
In comparison, one can leave the inputs and modify the hyperparameters instead. Approximation via hyperparameter optimization is a well-established research theme in machine learning. It's known there as 'learning to learn' or 'meta-learning'. I won't elaborate on this here and refer the reader to [5] simply because the paper title seems 'meta' enough.
Also noteworthy in the algorithm category is Capri [6]. There, the authors formulate knob tuning as a constrained optimization problem. To solve this problem, their proposed system learns cost and error models using bayesian networks.
Let's move now to application level approximation where we have to modify things inside the original algorithm. Compare this to the previous level where the original algorithm was an untouchable black-box. A good example here is loop perforation [7]. There, the authors identified certain loop patterns and propose techniques to automatically skip loop iterations.
For approximation at the architecture level, I refer to Quora [8]. Basically, the authors propose to extend the ISA of vector processors such that computation quality can be specified in the instruction set. Error precision is deterministically bound for each instruction.
Finally, there is approximation in hardware circuits. There are several proposals in the literature for approximate arithmetic units like adders and multipliers. They can be generally classified to deterministic (with reduced precision) and nondeterministic. Units of the latter type work most of the time as expected. However, they can occasionally produce arbitrary outputs.
The approximate circuits previously discussed are mostly designed manually for their specific purpose. In contrast, the authors of SALSA [9] approach hardware approximation from a different angle. They propose a general technique to automatically synthesize approximate circuits given golden RTL model and quality specifications.
I conclude this section by discussing how cost is expected to increase as we go from algorithm level to circuit level. Given a (correct) algorithm that exposes some configurable knobs. Adapting such algorithm to different settings is relatively cheap. Also, it can be highly automated based on established meta- optimization literature as can be found in meta-learning.
However, things get more challenging if we were to approximate outputs based on the internal workings of an algorithm. Generally, this application level approximation requires asking users for annotations or assumptions on expected inputs. Consequently, there is a smaller opportunity for automation and more difficulty in guaranteeing error quality.
The expected cost gets even higher at architecture level were several stakeholders might be affected. Compiler engineers, operating systems developers, and hardware architects all need to be either directly involved or at least aware of the approximation intended by the original algorithm developers. A proposed AC technique should demonstrate a serious value across the board to convince all of these people to get involved.
On nondeterministic approximate computing
Let's begin this section with a definition; An algorithm is considered to be nondeterministic if its output can be different for the same input. In a partially nondeterministic algorithm, nondeterminism sources can be feasibly accounted for a priori. Otherwise, the algorithm is considered fully nondeterministic.
Simulated annealing is an example of a partially nondeterministic algorithm where picking the next step is based on a random choice. Despite this, its control-flow behavior remain predictable which makes it relatively easy to reproduce implementation bugs with repeated runs. In contrast, the followed control-flow path can differ in 'unexpected' ways in the case of fully nondeterministic algorithms.
A nondeterministic AC technique introduces (or increases) nondeterminism in a given algorithm. This can be realized in several ways. In ApproxHadoop, the authors proposed random task dropping to gain more efficiency. Also, authors of SAGE [10] proposed skipping atomic primitives to gain performance at the expense of exposing the algorithm to race conditions.
Nondeterministic AC introduced by unreliable hardware has received special attention from the research community. This is motivated by the potential efficiency gains discussed already. I'll focus in the following on nondeterministic AC that is realized by unreliable hardware. Note that an algorithm is, typically, fully nondeterministic in this case.
There several possibilities to implement hardware-based nondeterministic AC. DRAM cells need a periodic refresh to retain their data which consumes energy. Equipping DRAMs with 'selective' no-refresh mechanisms saves energy but risks occasional bit errors.
Similarly, dynamically adapting bus compression and error detection mechanisms can provide significant gains in the communication between main memory and processing cores.
Additionally, there are efficiency opportunities in allowing processing cores themselves to provide a best-effort rather than a reliable service. In this setting, hardware engineers may optimistically invest in reliability mechanisms.
However, software programmers need, in turn, to be aware of hardware unreliability and invest in fault management schemes suitable for their particular needs. Relax [11] provide a good example of such an arrangement.
Also, CLEAR [12] provides an interesting design-space exploration of reliability against soft-errors across the entire system stack.
Despite the extensive research in reliability in general and more recently in AC. The problem of running software reliably and efficiently on unreliable hardware is far from solved. Beside the cost factor mentioned in the previous section, there are still major interdisciplinary problems to be addressed.
First, there is the abstraction problem of the hardware/software interface. Extending the ISA abstraction makes sense given its ubiquity. For example, each ISA instruction might be extended with probability specification. This probability quantifies how many times this nondeterministic instruction is expected to supply correct results (I'm becoming frequentist here).
However, microchip designs nowadays are complex possibly comprising tens of IP modules from several IP providers. It's difficult for a microchip manufacturer to derive such probabilities per individual instruction. Even where such derivation is possible, microchip manufacturers would be reluctant to guarantee such probabilities to their customers. Maintaining such guarantees through the entire product lifetime would prove costly.
Further, I think that it's still not clear how much value can this instruction-level abstraction provide to hardware as well as software engineers. Consequently, the question of finding suitable and generic abstractions between software and unreliable hardware is still open.
Second, there is the correctness challenge. Can we establish that a software running on nondeterministic hardware is correct or maybe probably correct? A short answer is probably no!
There are several reasons for this correctness challenge. Statistical correctness requires sampling from (joint) probability distributions of inputs which are typically not available a priori. Also, software functions are generally noncontinuous and nonlinear in the mathematical sense. This makes them good at hiding unexpected behaviors in the corners.
More importantly, algorithms process inputs in deterministic steps based on a specific control-flow. Nondeterministic hardware might affect control-flow decisions causing the algorithm to immediately fail, or worse, proceed and produce arbitrary outputs.
Note that the focus of this discussion is on the setting of a single computing node. Fault-tolerance in distributed systems consisting of many nodes is quite different. Although, the latter might be affected if individual nodes continue behaving unpredictably instead of just failing fast.
Let me elaborate based on the following code snippet. The function approximate
takes two inputs i1 and i2 and one hyperparameter input i3.
The latter is assumed to be a positive integer.
Local parameter k and i3
need to be protected (e.g., using software redundancy) otherwise the loop might not terminate.
1 2 3 4 5 6 7 8 9 10 | int approximate(int i1, int i2, int i3) {
int result = 0;
for(int k=0; k == i3; k++){
if(foo(i1) < bar(i2))
result += foo(i1)
else
result += bar(i2)
}
return result
}
|
The question now is what shall we do with functions foo and bar.
Leaving them unprotected means that we risk producing unpredictable value in result.
Note that a control-flow decision at line #4 is based on them.
This should provide a good reason for protecting them.
On the other hand, protecting foo and bar with software-based reliability
can prove more costly than running function approximate on deterministic hardware in the first place.
This is the essence of the control-flow wall.
Basically, decisions taken in the control-flow usually depend on the processed data. Guaranteeing data correctness is costly to do in software. On the other hand, allowing nondeterministic errors to affect data means that we can't, in general, guarantee how the algorithm would behave.
General-purpose programming on nondeterministic hardware was tackled in Chisel [13] (A successor for a language called Rely). The authors assume a hardware model where processors provide reliable and unreliable versions of instructions. Also, data can be stored in an unreliable memory.
There, developers are expected to provide reliability specifications. Also, hardware engineers need to provide approximation specification. The authors combine static analysis and Integer-Linear Programming in order explore the design-space while maintaining the validity of reliability specification. Still, their analyses are limited by data dependencies in the control-flow graph.
It's important to differentiate between the reliability specification in Chisel and the similar probabilistic specification of say Uncertain<T> [14]. The latter is a probabilistic programming extension to general-purpose languages. This means that the inputs are, typically, prior probability distributions that need to be processed deterministically .
That said, and without being able to guarantee (probable) correctness, would it make any sense to use nondeterministic hardware? Well, it depends. In the case where the cost of failure is small, and errors can't propagate deep into the program anyway, being failure oblivious might make sense [15].
Also, heterogeneous reliability, from my perspective, can make nondeterministic hardware a viable option in practice. Basically, reliable cores are used to run operating systems, language runtime, and programs. Only compute-intensive kernels/regions might be offloaded to accelerators which are possibly built using unreliable nondeterministic hardware. A notable example here is ERSA [16].
Conclusion
Improving efficiency is a continuous endeavor in all engineering disciplines. This endeavor requires balancing trade-offs between system cost and gained value. The goal is to obtain results that are good enough for the cost we invest.
Approximate computing is the research area where we attempt to realize techniques to automatically gain computing efficiency by trading off output quality with a metric of interest such as performance and energy. Automation is key to the value proposal of approximate computing as practitioners are able of manually balancing those trade-offs already.
Approximation also needs to be principled which allow practitioners to trust the system to behave as expected in the real world. Combining automation and principled guarantees is essential, in my opinion, for approximate computing to have a secure place in the engineering toolbox.
This article briefly introduced approximate computing. The discussion covered the entire system stack from algorithms to hardware circuits. Also, I elaborated a bit on nondeterministic approximation computing due to the special attention it received from the research community.
| [1] | S. Mittal, “A Survey of Techniques for Approximate Computing,” ACM Comput. Surv., vol. 48, no. 4, pp. 1–33, Mar. 2016. |
| [2] | Q. Xu, et al. “Approximate Computing: A Survey,” IEEE Des. Test, vol. 33, no. 1, pp. 8–22, Feb. 2016. |
| [3] | S. Chakradhar and A. Raghunathan, “Best-effort computing: Re-thinking Parallel Software and Hardware,” in Proceedings of the 47th Design Automation Conference (DAC ’10), 2010, p. 865. |
| [4] | I. Goiri, et al. “ApproxHadoop: Bringing Approximations to MapReduce Frameworks,” in Proceedings of the 20th International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS’15), 2015, vol. 43, no. 1, pp. 383–397. |
| [5] | M. Andrychowicz, et al., “Learning to learn by gradient descent by gradient descent,” preprint arXiv:1606.04474, 2016. |
| [6] | X. Sui, A. Lenharth, D. S. Fussell, and K. Pingali, “Proactive Control of Approximate Programs,” in Proceedings of the Twenty-First International Conference on Architectural Support for Programming Languages and Operating Systems (ASPLOS ’16), 2016, pp. 607–621. |
| [7] | S. Sidiroglou-Douskos, et al. “Managing performance vs. accuracy trade-offs with loop perforation,” in Proceedings of the 19th ACM SIGSOFT symposium and the 13th European conference on Foundations of software engineering (FSE’11), 2011, pp. 124–134. |
| [8] | S. Venkataramani, et al. “Quality programmable vector processors for approximate computing,” in Proceedings of the 46th Annual IEEE/ACM International Symposium on Microarchitecture - MICRO-46, 2013, pp. 1–12. |
| [9] | S. Venkataramani, et al. “SALSA: Systematic logic synthesis of approximate circuits,” in Proceedings of the 49th Annual Design Automation Conference on - DAC ’12, 2012, pp. 796–801. |
| [10] | M. Samadi, et al. “SAGE: self-tuning approximation for graphics engines,” in Proceedings of the 46th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO'46), 2013, pp. 13–24. |
| [11] | M. de Kruijf, et al. “Relax: an architectural framework for software recovery of hardware faults,” in Proceedings of the 37th annual international symposium on Computer architecture, 2010, pp. 497–508. |
| [12] | E. Cheng, et al. “CLEAR: Cross-Layer Exploration for Architecting Resilience: Combining Hardware and Software Techniques To Tolerate Soft Errors in Processor Cores,” in Proceedings of the 53rd Annual Design Automation Conference (DAC’16), 2016, p. 68. |
| [13] | S. Misailovic, et al. “Chisel: reliability- and accuracy-aware optimization of approximate computational kernels,” in Proceedings of the 2014 ACM International Conference on Object Oriented Programming Systems Languages & Applications (OOPSLA’14), 2014, pp. 309–328. |
| [14] | J. Bornholt, et al. “Uncertain< T >: a first-order type for uncertain data,” in Proceedings of the 19th international conference on Architectural support for programming languages and operating systems, 2014, pp. 51–66. |
| [15] | M. Rinard, et al. “Enhancing server availability and security through failure-oblivious computing,” in Proceedings of the 6th conference on Symposium on Opearting Systems Design & Implementation (OSDI’04), 2004, p. 21. |
| [16] | L. Leem, et al. “ERSA: Error Resilient System Architecture for Probabilistic Applications,” in Proceedings of the Conference on Design, Automation and Test in Europe (DATE'10), 2010, pp. 1560–1565. |